Interfacing MCP with Combinatorial, Convex, and SMT Solvers

Lately I've been working on using MCP beyond just using it for basic symbolic computer algebra manipulations, I've been thinking about how to interface large language models with a suite of dedicated solvers for scientific computing exposed as tools to the model. And particularly for automating workflows in physical engineering disciplines.

• Github Source Code
• git clone https://github.com/sdiehl/usolver.git

If you're not familiar with MCP, you can read more about it in my previous post or the thousand other breathless thinkpieces on the internet about how it's the greatest thing since sliced bread or something. But in reality it's just a janky way to expose a set of function calls (called tools) to a language model via a JSON RPC interface. Language are models are great at language interpretation and limited "planning", and numerical solvers are great at numerical computation. So let each system do what they do best and synthesize the two to build a hybrid system. MCP is just the glue to bind these scientific Python libraries with the model, essentially the 'cgi-bin' of AI.

The simplest motivation for combining language models with numerical solvers via MCP is that it's vastly more efficient for certain problems. Consider the dumb example that you certainly can feed a Sudoku puzzle into one of the frontier reasoning models (o3, deepseek r1, etc) and after spinning for quite some time it can (maybe) solve it by talking to "itself" about trial and error guesses for quite some time. The chain of thought will be this vast sequence of guesses and backtracking. But, you can also feed it into a dedicated numerical or logical solver and it will solve it nearly instantly. The same thing goes for many well-studied classical computer science problems: SAT, SMT, job shop, vehicle routing, knapsack problem, shift scheduling, travelling salesman etc. There are a lot of pre-existing efficient solvers.

As a less theoretical example, consider a common chemical engineering challenge: specifying the design parameters for a processing plant, focusing on line sizing and the associated fluid dynamics. In a typical day to day workflow engineers must determine optimal pipe diameters and requisite pump specifications to achieve target output flow rates for various chemical products. This task is essentially a system of coupled, often non-linear, governing equations encompassing fluid properties (density, viscosity), mass and energy balances across the network, and pressure drop calculations.

Any design must adhere to operational limits, such as maximum allowable pressures within each pipe segment to ensure structural integrity and safety, minimum flow rates to maintain reaction kinetics or prevent settling, and the physical topology of how pipes, valves, and reactors are interconnected. There are dedicated solvers for this, but they are very expensive, and generally suck. Or people write lots of Excel macros and Goal Seek, which I guess works, but there are much better tools.

The bottleneck is simply that the APIs for many of these open source SMT and convex solvers can be, let's say, character-building. If an LLM, piped through MCP, could translate your plain English "what if" into the arcane syntax these solvers speak, suddenly these super-powerful, often byzantine, systems become way less intimidating and democratize access beyond the need for relying on specialized programmers.

Imagine instead, just telling an LLM, via MCP: "Given these target flow rates for product X, using fluid Y with these properties, and ensuring pressure never exceeds Z psi in any line, what are the optimal pipe diameters and pump specs for lines A, B, and C, which are connected in this configuration? Imagine a process engineer who typically spends a significant portion of their week iteratively translating evolving production targets and safety parameters into precise mathematical constraints for solver input, then painstakingly validating the complex outputs for, say, a new heat exchanger network.

With an LLM-solver integration this same engineer could articulate high-level objectives and constraints in natural language—"design a network to cool stream X from 200°C to 50°C using available cold utility Y, minimizing operational cost while ensuring no tube-side pressure exceeds Z"—and have the system automatically formulate the problem, execute the appropriate solver, and present digestible design specifications. This could compress what was previously a multi-day, error-prone exercise as a human constraint generator and checker into minutes, liberating valuable engineering expertise to focus on genuinely creative challenges of their role.

And not just for this one specific field. The dream is to be able to describe all of the constraints for many complex systems (be it a chemical plant, hospital shift planning, or portfolio optimization) in natural language so that the LLM can plan the constraints, delegate to the solver(s), and let the user have a back and forth with about the problem and solution in way that is natural to them. If done well (and we're not there yet) that would be very very powerful.

Then there's more... let's call it forward-looking play: generating synthetic reasoning data. This one's a bit more niche. If we can get an LLM to bulk formulate tricky problems for these solvers, and then learn from the solver's perfectly structured, provably correct answers, we could bootstrap a ton of high-quality training data and then feed that back in as instruction tuning data.

Prototype

But let's start with the easy ones. That's the Stanford cvxopt for convex optimization, Microsoft's z3 SMT solver, and Google or-tools for combinatorial optimization. Just these three packages alone are extremely powerful. Like a seashell, if you look at their source code you can hear the screams of hundreds of PhD students sacrificed on the altar of science to build them.

I've built a prototype of this called USolver which implements the MCP interface to the solvers.

Let's look at some examples. For chemical engineering problems, you can describe a water transport pipeline design task in plain English which gets turned into a Z3 constraint satisfaction problem.

Design a water transport pipeline with the following requirements:

* Volumetric flow rate: 0.05 m³/s
* Pipe length: 100 m
* Water density: 1000 kg/m³
* Maximum allowable pressure drop: 50 kPa
* Flow continuity: Q = π(D/2)² × v
* Pressure drop: ΔP = f(L/D)(ρv²/2), where f ≈ 0.02 for turbulent flow
* Practical limits: 0.05 ≤ D ≤ 0.5 m, 0.5 ≤ v ≤ 8 m/s
* Pressure constraint: ΔP ≤ 50,000 Pa
* Find: optimal pipe diameter and flow velocity

The LLM translates this into a Z3 constraint satisfaction problem, handling all the messy details of flow equations and physical constraints. You get back optimal pipe dimensions and flow parameters that satisfy all your requirements.

Or take a classic operations research problem like employee scheduling. Instead of wrestling with complex combinatorial optimization syntax, you can just say:

Use usolver to solve a nurse scheduling problem with the following requirements:

* Schedule 4 nurses (Alice, Bob, Charlie, Diana) across 3 shifts over (Monday, Tuesday, Wednesday)
* Shifts: Morning (7AM-3PM), Evening (3PM-11PM), Night (11PM-7AM)
* Each shift must be assigned to exactly one nurse each day
* Each nurse works at most one shift per day
* Distribute shifts evenly (2-3 shifts per nurse over the period)
* Charlie can't work on Tuesday.

But where it gets really interesting is when you chain these solvers together. Here's an example where we optimize a restaurant's operations by combining two different solvers in sequence. First, we use Google's OR-Tools combinatorial optimization to determine the optimal mix and layout of different sized tables within a restaurant's available dining area, maximizing total seating capacity while respecting minimum table requirements and space constraints.

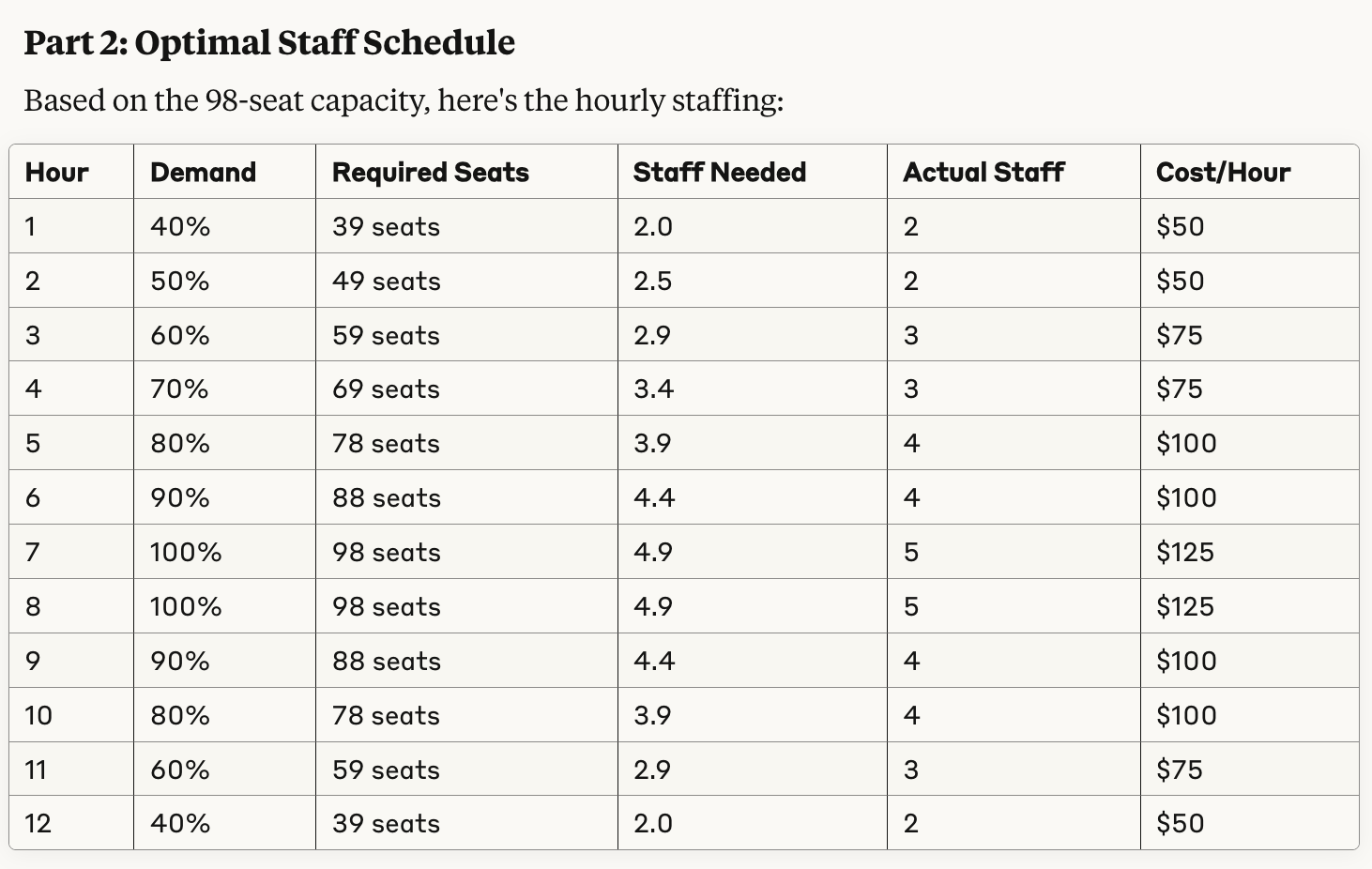
Then, we take that optimal seating capacity and feed it into the cvxopt solver to determine the most cost-effective staffing schedule across a 12-hour day. The staffing optimizer accounts for variable customer demand throughout the day, ensures adequate coverage for the calculated seating capacity, and minimizes labor costs while maintaining service quality and reasonable shift changes. This demonstrates how we can specify a a business problem in plain English, compile it down into a system of constraints, turn those constraints into a system of equations, and then solve it using a chain of numerical solvers with the LLM orchestrating the flow of data and verbalizing the answers!

Use usolver to optimize a restaurant's layout and staffing with the following requirements in two parts. Use combinatorial optimization to optimize for table layout and convex optimization to optimize for staff scheduling.

* Part 1: Optimize table layout
  - Mix of 2-seater, 4-seater, and 6-seater tables
  - Maximum floor space: 150 m²
  - Space requirements: 4m² (2-seater), 6m² (4-seater), 9m² (6-seater)
  - Maximum 20 tables total
  - Minimum mix: 2× 2-seaters, 3× 4-seaters, 1× 6-seater
  - Objective: Maximize total seating capacity

* Part 2: Optimize staff scheduling using Part 1's capacity
  - 12-hour operating day
  - Each staff member can handle 20 seats
  - Minimum 2 staff per hour
  - Maximum staff change between hours: 2 people
  - Variable demand: 40%-100% of capacity
  - Objective: Minimize labor cost ($25/hour per staff)

And then almost like magic, the LLM coordinates the two solvers and returns the optimal solution. It figures out the optimal table layout and then uses that to schedule the staff. Here's what Claude Desktop generates given the project specification.

And then figures out the optimal staffing schedule for that optimal table layout.

And it's pretty magical that such a complex problem can be solved in a few seconds with such a simple interface. I'm incredibly bullish about this kind of approach and expanding the set of available tools for the LLM to include many more advanced solvers.

Although don't drink too much of the breathless AI Kool-aid just yet. There are some quite real limitations in this approach. Namely, that there is no strict guarantees that LLMs are able to do semantic parsing of the problem with complete accuracy. We can partially mitigate this exposing a computer algebra system and having it check the solutions at each step. But there are still mechanisms for transpotitions and misinterpretations to slip in.

If this kind of approach becomes mainstream, there could also be benchmarks like SWE-bench for tool-calling of scientific computing packages that could be used to improve model performance upstream. But at the moment it's still very much a best-effort approach and you would certainly need to have a human-in-the-loop to check the solutions, especially in any kind of safety-critical application. But it might be able to make that human a lot more productive.

The Vision for Universal Solver Interface

Consider the potential of a unified interface that could seamlessly integrate with state-of-the-art solvers across multiple domains with frontier language models via MCP (or whatever the next generation of MCP is):

• Z3 - SMT solver for constraint satisfaction over booleans, integers, reals, and strings
• CvxPy - Framework for convex optimization problems
• Or-Tools - Suite for combinatorial optimization and constraint programming
• MiniZinc - Discrete optimization solver
• Clingo - Answer set programming system
• Flint - Number theory computations
• TLA+ / Apalache - Temporal logic solver
• Egglog - Term rewriting and equality saturation engine
• SymPy - Comprehensive computer algebra system
• Souffle - Datalog-based declarative logic programming framework
• Mathematica - Advanced symbolic mathematics system
• Sage - Umbrella project for many scientific computing packages

The implementation of such a unified system would be a very powerful and useful piece of software. It would effectively be a meta-solver: an intelligent system capable of decomposing complex problems, identifying the optimal solver for each component, and orchestrating their collective execution. While developing a theoretically complete meta-solver is a substantial theoretical and practical challenge in it's generality, don't really need to solve the general problem to be incredibily useful.

This project started as a weekend hobby project, but I believe this is a fascinating area with significant potential. I'm particularly interested in how these techniques could be applied to automation in physical engineering disciplines. If you're working on similar ideas in an open source or commercial context, I'd love to hear about your work, feel free to reach out.